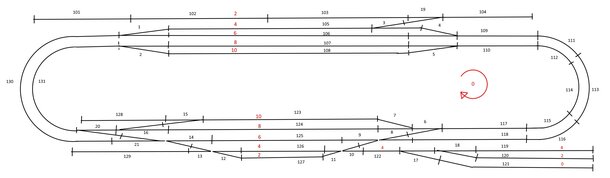
Itinéraires
Combien y-a-t-il d’itinéraires dans ce réseau ?
Pour l’instant, je ne sais pas.
Mais c’est l’Arduino qui va m’aider à trouver la réponse. Donc, parmi les 4 nombres que je cherche encore pour adapter le programme au réseau, le premier est très simple :
C’est le nombre maximal d’aiguilles dans un itinéraire donné.
Ici, le plus long itinéraire compte 5 aiguilles :
131 — 20 — 16 — 14 — 13 — 12 — 127
Il y a d’autres itinéraires à 5 aiguilles, mais aucun à 6.
Donc MAX_TURNOUT_ROUTE = 5. (nombre maximum d’aiguilles dans un itinéraire)
Les 3 autres concernent les 3 objets itinéraire. Et là, il faut détailler.
Comment demander un itinéraire au TCO ?
J’ai cherché la méthode la plus simple pour demander un itinéraire :
Pour demander l’itinéraire ci-dessus, j’appuie d’abord sur le BP (bouton poussoir) 131.
Je laisse le doigt sur le BP 131 et j’appuie sur le BP 126.
L’itinéraire s’affiche sur le TCO entre les 2 BP.
Je relâche les 2 BP et c’est fini, il est noté dans les itinéraires demandés.
En réalité, le TCO est ici théorique : le résultat est envoyé par le programme sous forme de liste sur le terminal de l’IDE Arduino.
Et si je ne veux plus de l’itinéraire démarrant en 131 ?
J’appuie simplement sur le BP 131 : tout itinéraire démarrant par la voie 131 s’efface.
Le premier objet itinéraire recense tous les itinéraires demandés.
Combien y’en a-t-il au maximum ?
Comme on n’en sait rien, autant le demander au programme.
On met au départ MAX_W_ROUTE à 100, par exemple. Un nombre dont on sait qu’il est trop grand.
On fait tourner le programme, on lui demande d’afficher la liste des itinéraires possibles et on regarde à partir de quand cette liste est vide, c’est à dire quand une ligne est complètement remplie de zéros.
Sur ce réseau, on trouve 35 lignes valides.
Fig 1 : Copie d’écran de ce qu’affiche la sortie sur le moniteur série
En noir : l’affichage lui même
En rouge : les significations des lignes et des colonnes
Surligné : les lignes qui serviront par la suite
Donc, MAX_W_ROUTE = 35. (nombre maximal d’itinéraires demandés (wanted))
Cette liste d’objets peut être complètement remplie. On ne s’occupe pas des incompatibilités.
On emmagasine simplement tout ce qui est demandé.
A noter également que les itinéraires sont orientés :
131 -> 126 n’est pas forcément identique à 126 -> 131.
Dans ce réseau, ce sont les mêmes puisqu’il n’y a qu’un chemin possible pour les deux.
Mais dans un réseau comme le mien qui aurait deux diagonales, ce ne serait pas vrai.
Il ne reste plus plus que deux variables spécifiques au réseau à renseigner.
On a donc la liste de tous les itinéraires demandés.
L’Arduino a calculé par quelles aiguilles ils passaient, sans s’occuper des autres itinéraires.
La méthode de calcul sera décrite plus tard.
On va construire la liste des itinéraires réservés.
Un itinéraire réservé est un itinéraire qui peut être réellement utilisé sur le réseau ;
Il y en a évidemment nettement moins que d’itinéraires demandés.
Il s’agit de déterminer le maximum d’itinéraires compatibles, sans les calculer.
Par exemple, pour les cantons 131, 107, 108 et l’aiguille 2, on ne peux avoir qu’un itinéraire sur les 4 possibles (131 —> 107, 131 —> 108, 107 —>131 et 108 —> 131). Donc un seul objet suffit.
On voit qu’il faut s’occuper essentiellement des aiguilles côté pointe.
La liste des itinéraires réservés est donc au maximum :
130 — 1
131 — 2
109 — 4
104 — 19
110 — 5
117 — 6
118 — 8
122 — 17
131 — 20
130 — 21
128 — 15
129 — 13
Donc MAX_R_ROUTE = 12 (Nombre maximum d’itinéraires réservés).
C’est là qu’on peut traiter des priorités
L’ordre dans lequel on rédige cette liste sera l’ordre dans lequel les itinéraires seront calculés. C’est ainsi qu’on gère les priorités.
Dans la liste des itinéraires demandés, certains utilisent les mêmes aiguilles.
Ce n’est pas un problème dans les itinéraires demandés.
Mais ça le devient quand on veut les réaliser sur le terrain.
Donc, si je juge que les voies vers Paris sont prioritaires, je vais commencer par réaliser cet itinéraire.
Ainsi, les aiguilles de cet itinéraire seront réservées, empêchant les autres itinéraires de les réserver.
C’est une gestion des incompatibilités dynamique !
Les vrais itinéraires :
A noter que, jusqu’à présent, on n’a fait que gérer des variables, aucune aiguille n’a bougé. Et, pour cet article, ça va continuer.
A partir des résultats de la liste des itinéraires réservés, on va pouvoir lancer la fabrication réelle des itinéraires.
Il faut donc renseigner un objet ROUTE qui va enregistrer la vraie position des aiguilles.
Et quand le processus est arrivé à terme, on va afficher VL et le train va (enfin !) pouvoir partir.
Autant les objets précédents ne tenaient pas compte de l’orientation des cantons, autant cet objet va être obligatoirement décrit dans le sens horaire, indépendamment du sens de circulation des trains. Cette disposition permet de simplifier la gestion des signaux.
Voici donc la liste :
130 — 1
131 — 2
103 — 19
105 — 3
106 — 4
107 — 5
108 — 5
117 — 6
118 — 8
119 — 18
120 — 18
121 — 17
123 — 15
124 — 16
125 — 14
126 — 12
127 — 12
Et, donc MAX_ROUTE = 17 (nombre maximal d’itinéraires dans le sens horaire).
Et maintenant, tout est décrit, le réseau et les itinéraires !
Le reste du programme, si compliqué soit-il, est universel.
Quel que soit le réseau, ce sera le même programme.
Le programme a toutes les infos spécifiques à votre réseau dont il a besoin pour faire tous les calculs, gérer tous les itinéraires, calculer tous les feux (jusqu’au panneau H) de tous les cantons dans les deux sens.
Et, par conséquence, afficher à tout instant, une vitesse maxi pour chaque train de votre réseau qui tiendra compte des positions des trains et des aiguilles.
Je ne saurais trop conseiller d’imprimer le contenu du dossier compressé.
Ces 5 fichiers vous aideront à comprendre la suite :
On y trouve, francisés, les fichiers :
- des cantons
- des aiguilles
- des itinéraires demandés
- de l’itinéraire en exemple
- et le plan du réseau.
Sous cette forme, tout est plus lisible.
Revenons au fonctionnement :
Tout d’abord, on appuie sur un BP.
Ce BP est, par exemple, relié à une entrée de l’Arduino MEGA qui gère la carte TCO.
Cette info est envoyée à la carte centrale par un bus CAN.
Le message CAN reçu par la carte centrale dans laquelle tourne le programme, appelle la fonction RouteChoice() qui va tester combien de BP sont appuyés.
Switch — case 1 :
Un seul BP est appuyé et on sait donc qu’il s’agit d’une origine d’itinéraire.
On appuie sur un deuxième BP.
Switch — case 2 :
Cette fois, 2 BP sont appuyés.
Quelque soit l’ordre dans lequel les BP sont testés, celui qui n’est pas le BP origine va être déclaré BP extrémité.
A cet instant, on fige le test des BP et on lance les calculs.
La carte centrale connait à cet instant à la fois l’origine et l’extrémité de l’itinéraire.
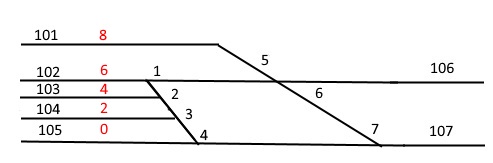
Par exemple 131 — 126.
Figure 2 : zoom sur la partie itinéraire de l’exemple.
Pour être plus précis, il s’agit de 131 côté 20 et de 126 côté 12.
Vous aviez certainement remarqué que, dans la liste des itinéraires demandés (wanted), il y avait deux 131 et deux 126 : 131 - 2, 131 - 20 et 126 - 12, 126 - 11.
On aura donc :
Pour 131 - 20, un message "33" reçu correspondant au 33ème objet de la liste.
En recevant "33", le programme va en déduire qu’on aborde l’aiguille 20 par le canton 131.
En regardant la liste des aiguilles, il va trouver que cette aiguille a les niveaux 8 et 7.
Niveau 8 si on va tout droit et niveau 7 si on tourne.
Pour 126 - 12, un message "26" reçu correspondant au 26ème objet de la liste.
En recevant "26", il va en déduire qu’on finit par le canton 126 qui se trouve au niveau 4 (via la liste des cantons).
Comme 8 > 7 > 4, c’est par la voie déviée qu’il faut aller vers 126.
La voie déviée de 20 est suivie par l’aiguille 21.
Comme on l’aborde en talon, il n’y a pas de choix : on sort par la pointe, c’est à dire par l’aiguille 14.
L’aiguille 14 est prise en pointe et se trouve avec les niveaux 6 (TD) et 5 (DV).
Comme 6 > 5 > 4, c’est par la voie déviée qu’on sort.
Aiguille 13 en talon, donc on va voir l’aiguille 12 qui a comme niveaux 4 et 3.
Comme 4 = 4, on sort par le canton 126 qui est le canton qu’on voulait atteindre.
Dans la liste, on trouve donc :
131
20 - 1 (1 = dévié)
21 - 1
14 - 1
13 - 1
12 - 0 (0 = tout droit)
126
Je n’ai pas décrit manuellement cet itinéraire et c’est le programme qui l’a trouvé tout seul en quelques microsecondes !
Nous avons maintenant une liste d’itinéraires demandés (jusqu’à 35 pour ce réseau).
Combien de BP pour commander tous les itinéraires du réseau ?
Tout dépend de la façon que vous aurez choisi pour interfacer votre réseau.
Si on continue à raisonner avec des BP, on serait tenté de répondre 35 ( = MAX_W_ROUTE).
Mais on ne va tout de même pas mettre 3 BP pour l’aiguille 1, toute seule !
Un seul BP pour une aiguille isolée.
A chaque appui sur le BP, on simulera l’appui sur le 2 BP sur lesquels il aurait fallu appuyer.
Cela deviendra une simple bascule :
1°) 131 — 107 par "34"+"6"
2°) 131 — 108 par "34"+"8"
Donc, au lieu des 9 BP "nécessaires" pour le fonctionnement des 3 aiguilles isolées (1, 2, 5), on n’en aura plus que 3, un par aiguille.
Donc il faudra 29 BP pour ce réseau.
L’itinéraire le plus court chemin n’est pas forcément le meilleur
Exemple :
Fig 3 : Exemple où le plus court chemin n’est pas forcément le meilleur
Un train arrive de 107 et va vers 102.
L’itinéraire le plus court est 107 — 7 — 6 — 5 — 1 — 102. Et il n’a que 4 aiguilles.
Mais si un train venant de 101 veut aller vers 106, il ne peut pas car les aiguilles 5 et 6 sont occupées.
Il aurait mieux fallu prendre 107 — 7 — 4 — 3 — 2 — 1 — 102 qui est pourtant plus long et qui a 5 aiguilles, soit une de plus.
L’itinéraire 101 — 5 — 6 — 106 serait maintenant possible.
Dans ma méthode :
L’aiguille 4 a comme niveaux 0 (TD) et 1 (DV)
L’aiguille 3 a comme niveaux 3 (TD) et 2 (DV)
L’aiguille 2 a comme niveaux 5 (TD) et 4 (DV)
L’aiguille 1 a comme niveaux 6 (TD) et 5 (DV)
L’aiguille 7 a comme niveaux 0 (TD) et 7 (DV), ce qui permet de prioriser la voie TD quand on va vers 102 à 105.
Maintenant, à vous de jouer !
Je fournis l’état actuel de mon programme qui, bien sûr est amené à évoluer.
Vous remarquerez qu’il est composé de plusieurs fichiers.
Le programme est scindé en différents objets, chacun traitant d’un sujet :
- Block.cpp et Block.h traitent des cantons
- Turnout.cpp et Turnourt.h traitent des aiguilles
- W_Route.cpp et W_Route.h traitent des itinéraires demandés
- R_Route.cpp et R_Route.h traitent des itinéraires réservés
- Route.cpp et Route.h traitent des itinéraires finaux
- Train.cpp et Train.h traitent de l’avancement des trains
- Variables.h regroupe toutes les variables globales
- Define.h regroupe tous les #define communs
Et, bien sûr le
- Gestion_Trains_Dom_108.ino qui commande tout.
Il faut extraire tous ces fichiers dans la même dossier, à placer dans le carnet de croquis de votre IDE.
Ce n’est pas à installer comme une bibliothèque.
En ouvrant le .ino, vous ouvrez simultanément tous les onglets.
programme est une version de simulation. Je travaille actuellement à l’intégration dans l’architecture de mon réseau.
Je ne manquerai pas dans l’avenir de vous faire part des évolutions.
Si c’est bien moi qui ai développé ce programme, je n’aurais pas pu le faire sans Thierry et Dominique.
Thierry d’abord grâce à ses articles sur la programmation objet :
Le monde des objets (1)
Le monde des objets (2)
Le monde des objets (3)
Puis en me donnant des pistes quand je bloquais sur des problèmes de syntaxe et de façon de raisonner dans le monde des objets.
Un grand merci, Thierry.
Et Dominique ensuite, qui m’a relu, corrigé, relu, donné des conseils, demandé des éclaircissements ...
Bref : qui a fait que les articles soient bien clairs et lisibles.
Un grand merci, Dominique.
Bon courage !
Je suis, bien sûr, à votre disposition pour toute question.
Suite (les cartes et leurs échanges) : SGDD (3) à paraître !